Stratigraphy and compaction¶
Stratigraphic record¶
Note
Stratigraphic architecture records surface evolution history from sediment production in the continental domain to its transport and deposition to the marine realm. To interpret stratigraphic architecture, gospl integrates the complete source-to-sink system: river erosion, sediment transport and deposition.
When the stratigraphic record option is turned on in gospl, stratigraphic layers are defined locally on
each partition and for each nodes and consist in the following information:
elevation at time of deposition,
thickness of each stratigraphic layer,
proportion of fine sediment if the dual lithology module is activated,
porosity of coarse sediment in each stratigraphic layer computed at centre of each layer, and
porosity of fine sediment in each stratigraphic layer computed at centre of each layer.
The model has the capability to consider two lithologies to simulate the first order behaviour of different sediment sizes on sediment transport and subsequent deposition. Specifically it allows to represent the efficiency of transport of fine grains against coarser ones in the marine environment by enabling the fine fraction to be transported over longer distances.
When the dual lithology is activated in gospl, the erosion, transport and deposition of the different proportions of sediments are recorded at any given time steps. This requires to keep track of the fine fraction in all layers previously deposited, and therefore is computationally much more demanding than simulation with only one sediment type. In this case, several assumptions are made. First, the model assumes that the volume of rock eroded using the stream power law accounts for both the solid and void phase. Second, the volume of each eroded lithology corresponds to the solid phase only and has the same composition (volume of fine versus coarse) as the eroded stratigraphic layers. Third, for sediment deposited inland in depression, the coarser sediments are deposited first and the finest sediments follow in case the depressions have not already been over-filled.
Inland deposits thicknesses and composition are then updated and recorded in the top stratigraphic layer and the porosities are set to uncompacted sediments values.
Porosity and compaction¶
To properly simulate stratigraphic evolution, sediment compaction is also considered in gospl as it modifies the geometry and the properties of the deposits.
Sediments compaction is assumed to be dependent of deposition rate and porosity \(\mathrm{\phi}\) is considered to varies with depth \(\mathrm{z}\) following the formulation proposed by Sclater and Christie, 1980 based on many sedimentary basins observations:
where \(\mathrm{\phi_0}\) is the surface porosity of sediments, and \(\mathrm{z_0}\) is the e-folding sediment thickness for porosity reduction.
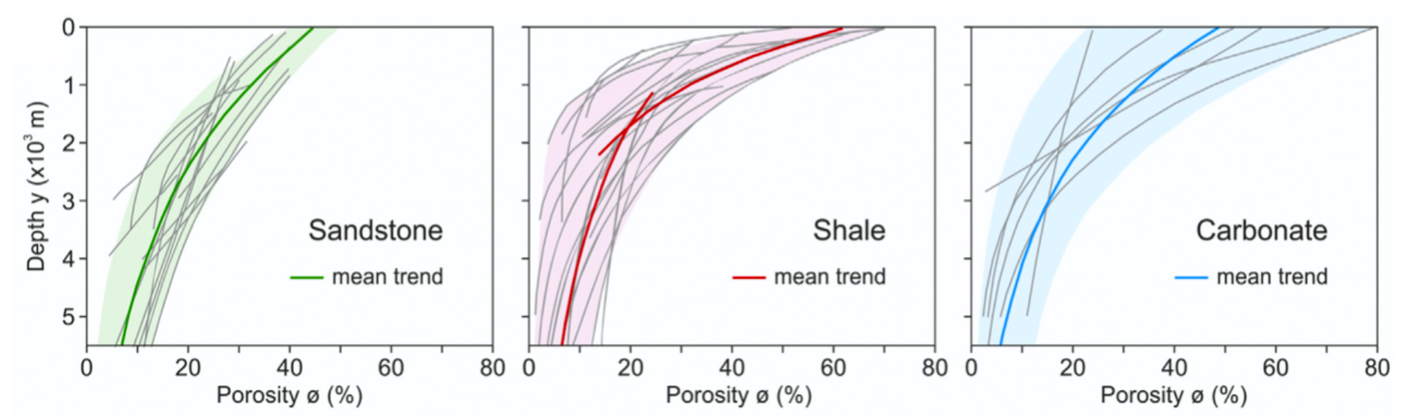
Fig. 5 Compilation plots of published compaction trends (grey lines) of sandstone, shale, carbonate (from Lee et al., 2020). The mean trend of each plot is defined by exponential function. A set of two exponential curves is applied to shale to fit better the underlying range.¶
As shown in the figure above, porosity decreases for burial depth of the order of a few thousand meters (\(\mathrm{z_0}\)), accordingly associated compaction increases substantially (Sclater and Christie, 1980). We can also see that the porosity and rate of compaction between fine and coarse sediments are significantly different. As a result, gospl uses the proportion of coarse versus fine at all depths within the underlying stratigraphy column to properly estimate compaction and induced elevation changes.
For a given stratigraphic layer \(\mathrm{i}\), the associated porosity for each sediment type is obtained at the centre of the layer for a specific depth \(\mathrm{\bar{z}_i}\) by:
At a given time \(\mathrm{k}\) after \(\mathrm{i}\), the layer centre depth is defined by:
where the thickness of that layer \(\mathrm{\Delta z_i^{k}}\) is related to the amount of solid material deposited in the layer \(\mathrm{\Delta h_{S,i}}\) by the following relationship:
where \(\mathrm{F_i}\) is the fraction of coarse sediment. The values of \(\mathrm{\Delta z_i^{k}}\) for \(\mathrm{i=1,...,k}\) are then computed sequentially from the top to the bottom of the sedimentary pile. Sedimentary layer elevation is then decreased based on the sum of compaction happening in each layer between two consecutive time steps.